What's really going to bake your noodle later on is, would you still have broken it if I hadn’t said anything?
What's really going to bake your noodle later on is, would you still have broken it if I hadn’t said anything?
 |
Main /
TutorialToric-codeThis tutorial has been contributed by Seyed N Saadatmand PrologueKitaev's toric code is a well-studied prototypical quantum stabilizer code, which is a good candidate, as a toy model, for understanding the intrinsic topological order and practicing tensor network simulations of a many-body system. Toric code is a model for strongly-correlated spins in a square lattice, placed on a torus. In this tutorial, we will learn how to construct the degenerate groundstates and applying global operation on them, using MPS and finite DMRG (fDMRG). Although real-world physical realization of the code proved to be challenging, but it can be taken as a purely mathematical concept capable of describing the building blocks of a topological fault-tolerant computer. A relevant key charectistic of topological orders is that the groundstate degeneracy depends on to the topology of the lattice. E.g., for a 2D model, if one places the lattice on a torus or a cylinder, the number of degenerate groundstates would be different. For some comprehensive introductions to the toric code and other quantum stabilizer codes refer to:
If you are planning for a simulation project on toric-code-related subjects, for inquiries on how to use the mp-toolkit for topological order calculations (in an optimized manner), you may contact me: Seyed N Saadatmand. Technical introductionConsider a {$ k \times k^\prime $} rectangular lattice on a torus. Spin-1/2 particles (or any other desired qubit) sit on edges. Consequently, the total number of accessible physical states is as {$ n=2^{kk^\prime} $}. You can see a schematic presentation of the toric code in the following figure. 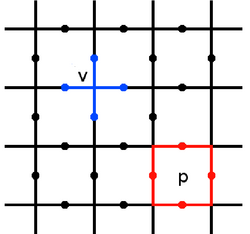 [Courtesy of Wikipedia] Toric Code schematic lattice with stabilizer operators We will show the stabilizer operators, acting in star and face plaquettes, with {$A_s$} and {$B_p$} respectively, which are defined as {$$ A_s= \prod_{j \in stars} \sigma_j^x, $$} {$$ B_p= \prod_{j \in faces} \sigma_j^z, $$} where the multiplication is over four sites of a plaquette. The toric code Hamiltonian for is {$$ H = -J_e \sum_s A_s -J_m \sum_p B_p, $$} where the sums are over all possible plaquettes. Henceforth, we set {$J_e=1, J_m=1$} for the sake of simplicity. The Hamiltonian contains four-body interactions, which causes long-range entanglement, but makes the model harder to simulate using numerical methods. For all vertice and face operators, on can write {$$ [A_s,B_p]=0, $$} since separated {$A_s$} and {$B_p$} commute, trivially, and those with shared sites can only have 0 or 2 common edges. It is noteworthy that, from Pauli matrices' properties, we know {$A_s$} and {$B_p$} are Hermitian with {$\pm1$} eigenvalues. If {$\Upsilon$} be the general Hilbert space (with total dimension {$ 2^{kk^\prime} $}), we define a protected groundstates' subspace as {$$ L=\{| \xi > \in \Upsilon :A_s| \xi >=| \xi >,B_p| \xi >=| \xi >, \vee s,p\}. $$} This can be considered as the definition of the quantum code of {$ TOR( k\times k^\prime) $}. The importance of toric code and other stabilizer quantum codes?There are many pedagogical reasons supporting the study of the toric code. However, the robust groundstate degeneracy of the model (protected against thermal and quantum noises), also offers potential applications for encoding information. SU(2)-symmetry of the spin systems may also offer a built-in symmetry-sector degeneracy to encode information. However, SU(2) symmetry can be simply lifted by a stray magnetic field [for more details, see arXiv:0904.2771v1 ]. |